上下界网络流大抵(蒟蒻wy只知道)有四种形式
1、无源汇判断是否有可行流
2、有源汇判断是否有可行流
3、有源汇最大/最小流
4、有源汇最大/最小费用流
一、无源汇判断可行流
对于一条边(u, v) 假设其流量上下界为[x, y]
则我们要求至少有x的流量经过
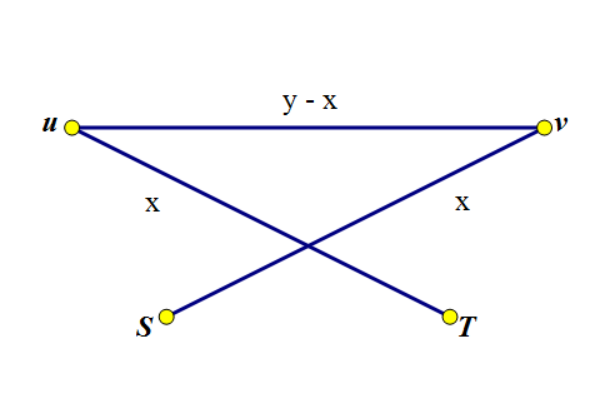
我们新建一个超级源点S和一个超级汇点T
连一条(u, T)容量为x的边 强制有x的流量流出u
连一条(S, v)容量为x的边 强制有x的流量流入v
那么如果这两条边流满 那么流量一定满足下界
反之如果这两条边未流满 流量就不满足下界
对于原图中(u, v)的边 将其容量改为y - x
由于经过边的流量f(u, v)一定不超过该边的容量c(u, v)
f(u, v) ≤ c(u, v)
所以 总流量一定不超过上界y
综上, 若(u, T), (S, v)均满流 则 该图对应一可行流法
在实际应用时 我们可以用degree[u] 表示流入点u的流量减去流出点u的流量
对于任一点u 判断degree[u] 与 0的大小关系
若degree[u] > 0 连(S, u)容量为degree[u]的边
若degree[u] < 0 连(u, T)容量为-degree[u]的边
对新图跑最大流
只需判断是否满足即可
二、有源汇判断可行流
有源汇判可行流直接从原来的汇点连一条无穷大的边到源点
将其转化为无源汇判可行流即可
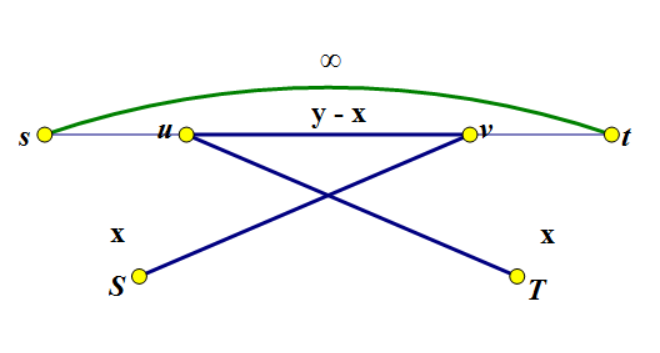
三、有源汇求最大/最小流
首先有最大最小流的必要条件是原图要有一可行流
我们先判断是否有可行流 若无可行流则无解
否则 我们就得到一个循环可行流
事实上
可行流的循环流量就是流过(t, s)边的流量
即(t, s)边反向边的容量
Ps:因为只有边(t, s)是从t流向s构成循环的
设可行流流量为x
求最大流时
在残余网络中可能还有新的增广路
以原图的s, t为源汇 再跑一遍最大流
设最大流为y1
则 ans = x - y
对于最小流
考虑可行流可能多流了s到t的部分流量
我们从t到s跑最大流退流回去
注意到直接退流可能会使流不满足下界
我们将第一次跑流时超级源点S 和超级汇点T 连出的边及其反向边都删掉
这样保证流不会顺着这些边退回去导致不合法
设最大流为y0
则 ans = x - y0
四、有源汇最大/最小费用流
有源汇求最大/最小费用流的方法实际上与有源汇求最大/最小流的方法一样
但需要注意
对于强制边(u, T), (S, v)
两条中只要有一条的费用为(u, v)的费用w
两条费用均为w会导致错误
对于其他新增边(实际上就是(t, s)), 边的费用为0
 评论 (0)
评论 (0)