wy's Blog

4138: [FJOI2015]最小覆盖双圆问题

Description

给定平面上n个点(x1,y1),...,(xn,yn)，找出2个半径相同的圆R1和R2，覆盖给定的n个点，且半径最小。

 

设计一个算法，计算出所求最小覆盖双圆 R1 和 R2 的半径。

 

 

Input

Output

Sample Input

Sample Output

HINT

FJ2015省选题

正解wy是不会的，于是用一些奇怪的方法A过了（我不会告诉你我是骗过的）。。。

对于所有点，先按其x坐标排序。。。

然后二分出一个分界点，把点分成两堆。。。

分别做最小圆覆盖，两个半径的最大值即为该分法的答案。。。

向较大圆一边二分新的分界点，然后再求答案。。。

如果你觉得就这么简单，那你就太天真了。。。<(￣ˇ￣)/

由于我们是将点按x坐标排序的，

所以我们只能把点按与y轴平行直线分成左右两堆（如图1）。

那么问题来了，

如果答案是讲点按某一斜线分成两堆的（如图2），我们该怎么办呢？

←这是图1   这是图2 →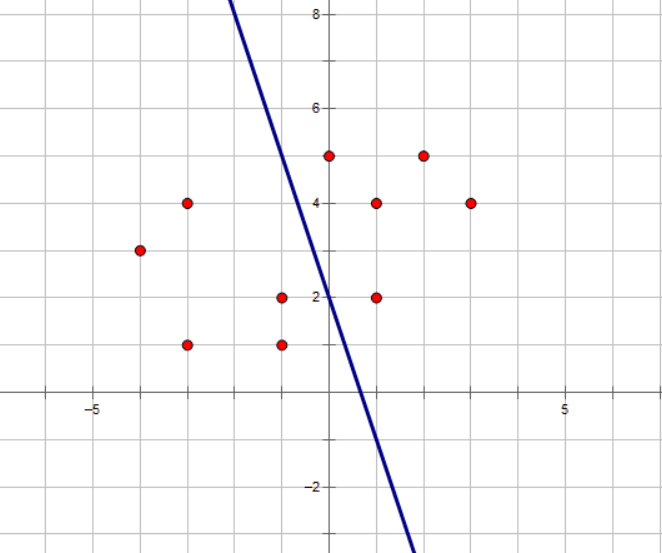 

这里有一个奇妙(pian fen)的方法：将平面直角坐标系旋转（其实就是旋转点）。。。

wy是每次转1°，转360次。。。（显然分得越细，答案越准确，但时间越长）

所以骗分算法确定了，

将平面直角坐标系不断旋转，

对于每个旋转后的图，

二分分界点后做两个最小圆覆盖并更新答案。。。

这里有两个优化

首先每次旋转时的三角函数计算是耗时巨大的。。。

所以我们应该先将它的值存下来（好吧，这应该只有蒟蒻wy才会忽略 O_O)

另一个比较重要，

当覆盖的两个圆中较小的的一个还是大于答案，这张图就不能更新答案了。。。

#include<cmath> 
#include<cstdio>
#include<algorithm>
using namespace std; 
const int MaxN=1010;
const double eps=1e-9,ki=1.0/180*acos(-1);  //角度制转弧度制    
const double co=cos(ki),si=sin(ki);         //cos(),sin()函数的自变量为弧度制 
int N;
double k,R,ans;
struct point{
	double x,y;
	inline point (double a=0,double b=0){
		x=a; y=b;
	}
}p[MaxN],a[MaxN],O;
inline point rotate(const point &a){
	point p;
	p.x=a.x*co-a.y*si;
	p.y=a.x*si+a.y*co;
	return p;
}
inline bool cmp(const point &a,const point &b){
	return a.x<b.x;
}
inline double dist(const point &a,const point &b){
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
inline bool In(const point &a){
	return dist(a,O)<=R+eps;
}
inline void QueryO(const point &a,const point &b,const point &c){
	double A=a.x*a.x-b.x*b.x+a.y*a.y-b.y*b.y,B=(b.x-a.x)*2,C=(b.y-a.y)*2;
	double D=c.x*c.x-b.x*b.x+c.y*c.y-b.y*b.y,E=(b.x-c.x)*2,F=(b.y-c.y)*2;
	O.x=(D*C-A*F)/(B*F-E*C);
	O.y=(D*B-A*E)/(C*E-F*B);
}
inline double Query(int l1,int l2){
	if (l1>l2) return 0;
	for (int i=l1;i<=l2;++i)
	    a[i]=p[i];
    random_shuffle(a+l1,a+l2+1);
	O=a[l1];
	R=0;
	for (int i=l1;i<=l2;++i)
	    if (!In(a[i])){
	    	O=a[i];
	    	R=0;
	    	for (int j=l1;j<i;++j)
	    	    if (!In(a[j])){
	    	    	O.x=(a[i].x+a[j].x)/2;
	    	    	O.y=(a[i].y+a[j].y)/2;
	    	    	R=dist(O,a[j]);
	    	    	for (int k=l1;k<j;++k)
	    	    	    if (!In(a[k])){
	    	    	        QueryO(a[i],a[j],a[k]);
	    	    	    	R=dist(O,a[k]);
						}
				}
		}
	return R;
} 
int main(){
	for (;;){
		scanf("%d",&N);
		if (N==0) break;
		ans=1e8;
    	for (int i=1;i<=N;++i)
            scanf("%lf%lf",&p[i].x,&p[i].y);
        for (int d=1;d<=360;++d){
        	for (int i=1;i<=N;++i) p[i]=rotate(p[i]);
        	sort(p+1,p+N+1,cmp);
        	int l=1,r=N;
        	for (;l<=r;){
        		int mid=(l+r)/2;
        		double r1=Query(1,mid);
        		double r2=Query(mid+1,N);
        		double an=r1>r2?r1:r2;
        		if (r1+r2-an>ans) break;   
        		ans=ans<an?ans:an;
        		if (r1<r2) l=mid+1;
        		else r=mid-1;
			}
		} 
	    printf("%.2lf\n",ans);
	}
}

Ps：同机房Q神犇表示不写inline是不可以过的，wy感觉很有道理。。。